How to Solve Natural Logarithms

 A Step-by-Step Guide

Natural logarithms (denoted as ln) are an essential mathematical concept, and understanding how to solve them is a crucial skill in algebra, calculus, and various other fields. How to Solve Natural Logarithms If you’re working with equations involving natural logs, this guide will walk you through the process of solving them, step by step. Whether you’re a student tackling homework or someone brushing up on math skills, this blog post will help simplify the steps involved in solving natural logarithmic equations.

What is a Natural Logarithm? How to Solve Natural Logarithms

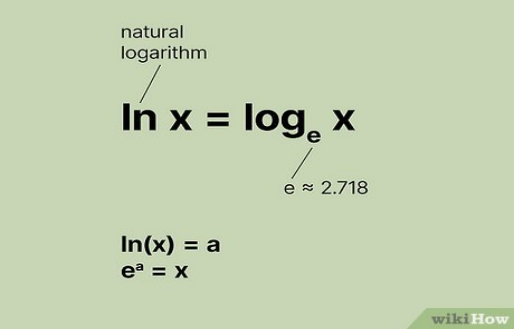
Before jumping into solving natural logarithmic equations, let’s briefly review what a natural logarithm is.

The natural logarithm is a type of logarithm with e (Euler’s number, approximately 2.718) as its base. It is denoted as ln(x), and it answers the question: “To what power must e be raised to produce the number x?”

For example:

• ln(e) = 1 because e^1 = e
• ln(e^x) = x because the natural log and e are inverse functions.

Key Rules to Remember for How to Solve Natural Logarithms

When solving natural logarithmic equationsHow to Solve Natural Logarithms, there are a few important logarithmic rules you should be familiar with:

1. Product Rule:

ln⁡(a)+ln⁡(b)=ln⁡(ab)\ln(a) + \ln(b) = \ln(ab)ln(a)+ln(b)=ln(ab)

When you add two natural logs, you can combine them by multiplying the terms inside the logarithms.

• Quotient Rule:

ln⁡(a)−ln⁡(b)=ln⁡(ab)\ln(a) – \ln(b) = \ln\left(\frac{a}{b}\right)ln(a)−ln(b)=ln(ba​)

When you subtract two natural logs, you can combine them by dividing the terms inside the logarithms.

• Power Rule:

ln⁡(ab)=b⋅ln⁡(a)\ln(a^b) = b \cdot \ln(a)ln(ab)=b⋅ln(a)

If you have an exponent inside the natural log, you can bring the exponent out as a multiplier.

Steps for Solving Natural Logarithmic Equations

Now that we understand the basics of natural logarithms and the key rules, let’s break down the steps for solving an equation involving natural logs.

Step 1: Simplify the Natural Log Expressions

The first thing you should do when solving a natural logarithmic equation is to simplify the terms inside the natural logarithms. How to Solve Natural Logarithms This might involve using the product rule, quotient rule, or power rule. The goal is to combine or simplify the logs to make the equation easier to solve.

Example:

If you have the equation:

ln⁡(x)+ln⁡(3)=ln⁡(6)\ln(x) + \ln(3) = \ln(6)ln(x)+ln(3)=ln(6)

Use the product rule to combine the left side:

ln⁡(3x)=ln⁡(6)\ln(3x) = \ln(6)ln(3x)=ln(6)

Step 2: Eliminate the Natural Log

Once you’ve simplified the equation, the next step is to eliminate the natural log. Since ln(x) is the inverse of e^x, you can “cancel out” the natural logarithm by raising both sides of the equation to the power of e. This step is crucial because it transforms the equation into a simpler algebraic form that’s easier to solve.

Example:

From the equation:

ln⁡(3x)=ln⁡(6)\ln(3x) = \ln(6)ln(3x)=ln(6)

Raise both sides of the equation to the power of e:

eln⁡(3x)=eln⁡(6)e^{\ln(3x)} = e^{\ln(6)}eln(3x)=eln(6)

Since e^ln(x) = x, the equation becomes:

3x=63x = 63x=6

Step 3: Solve the Resulting Algebraic Equation

Now that the natural log has been eliminated, How to Solve Natural Logarithms you’re left with a basic algebraic equation. You can now solve for the unknown variable just like you would in any other algebraic equation.

Example:

From the equation:

3x=63x = 63x=6

Divide both sides by 3:

x=2x = 2x=2

This is the solution to the equation!

Special Cases: What if There’s No Solution?

Not every equation involving natural logarithms will always have a solution. How to Solve Natural Logarithms If you encounter an equation where the terms inside the natural log become negative or zero, then the equation has no solution. This is because the natural logarithm is only defined for positive real numbers. For instance:

ln⁡(x)=ln⁡(−3)\ln(x) = \ln(-3)ln(x)=ln(−3)

Since ln(x) is undefined for negative values of x, this equation has no solution.

Example Problems to Practice

Problem 1: Using the Product Rule

Solve for x:

ln⁡(2x)+ln⁡(5)=ln⁡(20)\ln(2x) + \ln(5) = \ln(20)ln(2x)+ln(5)=ln(20)

Step 1: Apply the product rule:

ln⁡(10x)=ln⁡(20)\ln(10x) = \ln(20)ln(10x)=ln(20)

Step 2: Eliminate the natural log by raising both sides to the power of e:

10x=2010x = 2010x=20

Step 3: Solve for x:

x=2x = 2x=2

Problem 2: Using the Quotient Rule

Solve for x:

ln⁡(x+3)−ln⁡(x−1)=2\ln(x + 3) – \ln(x – 1) = 2ln(x+3)−ln(x−1)=2

Step 1: Apply the quotient rule:

ln⁡(x+3x−1)=2\ln\left(\frac{x + 3}{x – 1}\right) = 2ln(x−1x+3​)=2

Step 2: Eliminate the natural log by raising both sides to the power of e:

x+3x−1=e2\frac{x + 3}{x – 1} = e^2x−1x+3​=e2

Step 3: Solve for x:
Multiply both sides by (x – 1):

x+3=e2(x−1)x + 3 = e^2(x – 1)x+3=e2(x−1)

Distribute the e^2:

x+3=e2x−e2x + 3 = e^2x – e^2x+3=e2x−e2

Move the x terms to one side:

x−e2x=−e2−3x – e^2x = -e^2 – 3x−e2x=−e2−3

Factor out x:

x(1−e2)=−e2−3x(1 – e^2) = -e^2 – 3x(1−e2)=−e2−3

Solve for x:

x=−e2−31−e2x = \frac{-e^2 – 3}{1 – e^2}x=1−e2−e2−3​

Conclusion

Solving natural logarithms doesn’t have to be intimidating. By following these steps—simplifying the expression, eliminating the natural log, and solving the resulting algebraic equation—you can confidently solve any equation involving natural logarithms. Just remember to apply the product, quotient, and power rules where appropriate, and don’t forget to check for solutions that make sense within the domain of the natural logarithm (positive values only). How to Solve Natural Logarithms

With practice, you’ll become more comfortable and efficient at solving natural logarithmic equations. Happy solving!